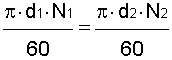Relación de transmisión

Correas y poleas

N = Numero de revoluciones por minuto
d = Diámetro de las poleas
Al estar en marcha, las dos poleas tendrán la misma velocidad tangencial (m/seg), manteniéndose la siguiente igualdad:

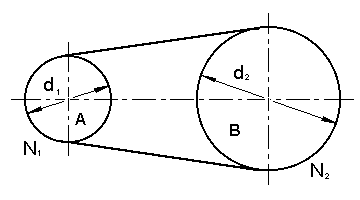simplificando nos queda

deduciéndose la siguiente proporción donde i es la relación de transmisión.

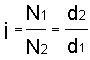
Ejemplo: La rueda A gira a 2400 rpm. y tiene un diámetro de 95 mm. Hallar las revoluciones de la rueda B si esta tiene 225 mm. de diámetro.

despejando de la formula de la relación de transmisión tenemos

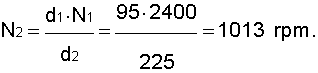
Engranajes

N = Numero de revoluciones por minuto
d = Diámetro primitivo de la rueda dentada
En un sistema de engranaje la velocidad tangencial a la altura de los diámetros primitivos es igual en las dos ruedas, por lo tanto:

ecu16.gif (608 bytes)

simplificando nos queda

lo que nos permite expresar la relación de transmisión i de un engranaje en función de los diámetros primitivos de sus ruedas.

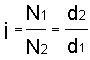
Puesto que en un engranaje las dos ruedas han de tener el mismo módulo, es fácilmente deducible que sus diámetros primitivos son directamente proporcionales al número de dientes:

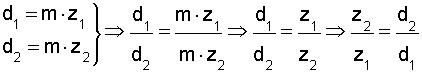
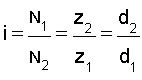
lo que nos permite expresar la relación de transmisión i de un engranaje en función de numero de dientes de sus ruedas:

Ejemplo: Un motor gira a 2.500 rpm. transmitiendo el movimiento a un eje mediante un engranaje de un piñón de 35 dientes solidario al eje de giro del motor. Si queremos que el eje al que se transmite el movimiento gire a 486 rpm. que numero de dientes ha de tener la rueda conducida.

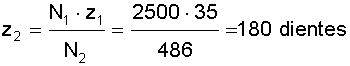
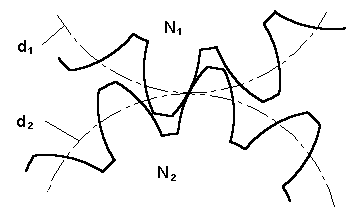
Tren de engranajes

La relación de transmisión en un tren de engranajes es igual al cociente que resulta de dividir el producto de los números de los dientes de las ruedas conducidas entre el producto de los números de dientes de las ruedas conductoras.

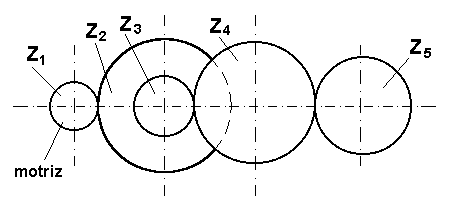En el tren de la figura, z₁ mueve a z₂. Esta gira solidaria con z₃ que a su vez mueve a z₄ y esta última a z₅ , con lo que z₄ es a la vez conducida y conductora.

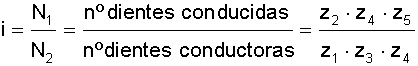
Ejercicios

Ejercicio 1.

Calcular las revoluciones por minuto de la rueda z₅ de la figura anterior si el eje motriz gira a 1350 rpm. y los dientes de las ruedas son z₁ = 35; z₂ = 95; z₃ = 40; z₄ = 85; z₅ = 75.

Solución: La rueda z₅ gira a 265,26 rpm.

Ejercicio 2.

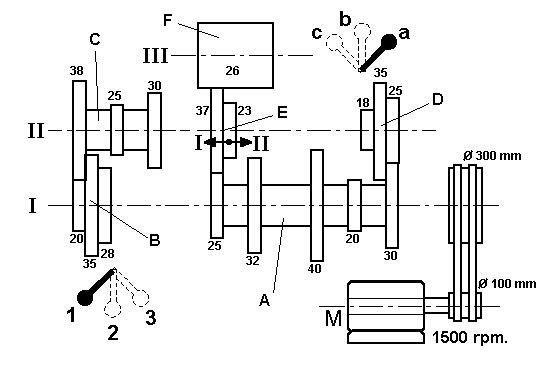
Calcular todas las velocidades del eje III ,en revoluciones por minuto, de la siguiente caja de velocidades cuyo funcionamiento es el siguiente:

El motor M transmite el movimiento al eje I mediante un par de poleas, este a su vez mueve el grupo de ruedas dentadas B que gira solidario a el. Este grupo mueve al grupo C que gira solidario al eje II que a su vez mueve el grupo de ruedas D. Este grupo mueve al grupo A que gira libre en el eje I y que transmite el movimiento al grupo E que gira libre en el eje II. El grupo E finalmente mueve al eje III a través de la rueda F que gira solidaria a el.

El grupo de ruedas B tiene 3 posiciones 1-2-3. El grupo de ruedas D tiene 3 posiciones a-b-c.
El grupo de ruedas E tiene dos posiciones I - II.

Solucion:

I		a	b	c
	1	210	442	113
	2	560	1177	302
	3	373	783	200
II	1	433	911	234
	2	1154	2425	623
	3	768	1614	415