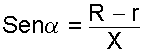| |
Conos |
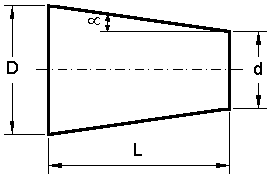
Magnitudes características de un cono
| Geométricamente, un tronco de cono queda definido al conocer el diámetro de su base mayor "D", el diámetro de su base menor "d", y su altura o longitud "L". A fin de facilitar la construcción y verificación se emplean unas magnitudes características que se pueden resumir en:
|
|
Conicidad
Es la variación de diámetro que experimenta un cono por unidad de longitud. Se representa por "c".
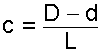
En ocasiones la conicidad puede referirse la longitud de 100 mm., denominándose en este caso conicidad porcentual.Se representa por "cp".
cp = 100 · c
Inclinación
Es la variación de radio que experimenta un cono por unidad de longitud. Se representa por "i".
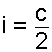
Ángulo de inclinación
Es el formado por el eje del cono y una generatriz. Se representa por "µ".
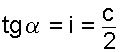
La tangente del ángulo de inclinación es igual a la inclinación e igual a la mitad de la conicidad.
Ángulo en el vértice
Es el formado por dos generatrices opuestas, deduciéndose de esta definición que es igual al doble del ángulo de inclinación.
Determinación de las magnitudes características
Conos exteriores.- Su medición exige disponer de los siguientes elementos
| Cuatro calas, iguales dos a dos. | |
| Cuatro varillas iguales de diámetro calibrado "d0". | |
| Un instrumento de medición lineal (pie de rey o micrómetro). |
1. Se sitúa la pieza con su base menor apoyada sobre el mármol. A continuación se colocan las calas y sobre ellas las varillas de diámetro d0 , de forma que estas queden tangentes a dos generatrices diametralmente opuestas del tronco de cono.
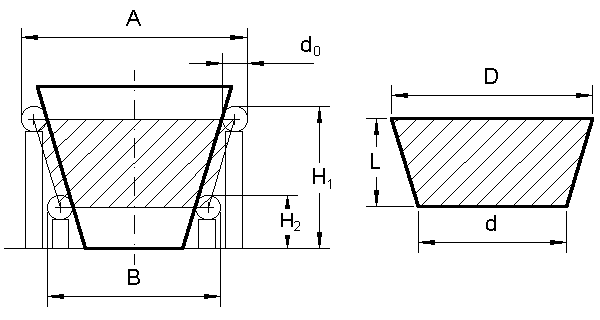
Figura 1
2. Se determinan los diámetros D y d correspondientes a las bases del tronco de cono comprendido entre los centros de las varillas superiores y de las inferiores. Para ello de la observación de la figura se deduce que:
D = A - d0 ; d = B - d0 ; L = H1 - H2
3. Conocidos los valores de D, d y L se calcula el ángulo de inclinación del cono.
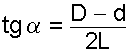
Conos interiores.- Su medición exige disponer de los siguientes elementos:
| Dos bolas calibradas de radios conocidos "R" y "r". | |
| Un instrumento de medición lineal (pie de rey o micrómetro). |
| Situada la pieza con su base menor apoyada en el mármol, las bolas se colocan según se detalla en la figura. De la observación de la figura, se deduce que :
|
|
Ejercicios
| 1. | Calcular el diámetro menor de un cono, sabiendo que su diámetro mayor es 80 mm; su longitud, 196 mm; y su conicidad porcentual, del 5 %. | 70,2 mm |
| 2. | Calcular el diámetro mayor de un cono, sabiendo que su diámetro menor mide 25 mm; su longitud, 62 mm; y su ángulo de inclinación, 10°. | 46,86 mm |
| 3. | En la determinación de las magnitudes características
de un cono interior se han utilizado dos bolas de 10 y 5 mm de radio, habiéndose obtenido
en la medición de las alturas los siguientes valores: H1 = 425,86 mm; H2 =228,18 mm. Calcular la conicidad porcentual del cono. |
5,192 % |
| 4. | Al medir las dimensiones A y B de la pieza representada en la figura 1, se han obtenido los siguientes valores: A = 92,13 mm; B = 58,06 mm. Calcular la conicidad sabiendo que se han utilizado calas de 12 y 45 mm de altura, y varillas de 10 mm de diámetro. | 1,0324 |
| 5. | Calcular el ángulo en el vértice de la pieza
representada en la figura 2, sabiendo que se han utilizado bolas de 25 y 15 mm de radio, y
que en la medición de las alturas se han obtenido los siguientes valores, H1 = 88,37 mm; H2 = 36,15 mm. |
27º 24' |
© Roberto de Diego
![]()