| |
Trigonometría |
Trigonometría es la parte de las Matemáticas que tiene por objeto el estudio de los triángulos, determinando el valor de sus ángulos y lados.
Razones trigonométricas
Para cualquier ángulo, se consideran seis razones trigonométricas:
|
|
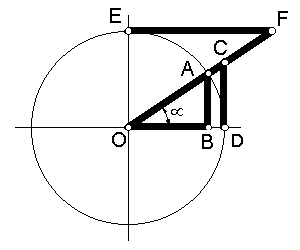
Considerando el triángulo rectángulo OAB de la figura 1 tenemos que para el ángulo µ:
Seno es el cociente entre el cateto opuesto al ángulo µ AB, y la hipotenusa OA.
Coseno es el cociente entre el cateto contiguo al ángulo µ OB, y la hipotenusa OA.
Tangente es el cociente entre el cateto opuesto AB y el cateto contiguo OB.
Cotangente es el cociente entre el cateto contiguo OB y el cateto opuesto AB.
Secante es el cociente entre la hipotenusa OA y el cateto contiguo OB.
Cosecante es el cociente entre la hipotenusa
OA y el cateto opuesto AB.
|
|
|
Si se toma el radio como unidad las razones trigonométricas reciben el nombre de líneas trigonométricas, de este modo:
![]()
y como consecuencia las líneas trigonométricas son:
Relaciones fundamentales
| sen2 µ + cos2 µ = 1 |
 |
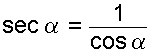 |
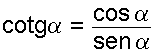 |
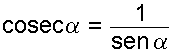 |
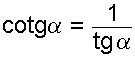 |
Resolución de triángulos rectángulos
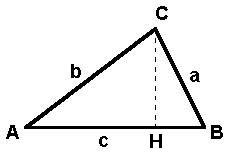
Consideremos un triángulo rectángulo definido por el ángulo recto A, los ángulos agudos B y C, los catetos b y c, y la hipotenusa a.
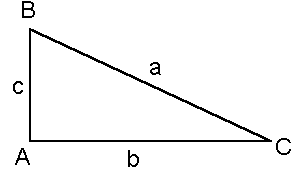
Figura 2
En todo triángulo rectángulo se cumple que:
La suma de los dos ángulos agudos es 90º.
B + C = 90º
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (Teorema de Pitagoras)
a2 = b2 + c2
Un cateto es igual al producto de la hipotenusa por el seno del ángulo opuesto.
Un cateto es igual al producto de hipotenusa por el coseno del ángulo comprendido entre ambos.
Un cateto es igual al producto del otro cateto por la tangente del ángulo opuesto al primero.
Casos de resolución de triángulos rectángulos
Un triángulo rectángulo puede venir definido por :
|
A continuación, por medio de ejemplos, veamos la forma de solucionar cada uno de los cuatro casos.
1. En el triángulo ABC de la figura 2, definido por la hipotenusa a = 5 m, y el ángulo C = 37º, determinar los restantes elementos:
El ángulo B será: B = 90º - C = 90º - 37º = 53º
El cateto b será: b = a · cos C = 5 · cos 37º = 5 · 0,79864 = 3,993 m
El cateto c será: c = a · sen C = 5 · sen 37º = 5 · 0,60182 = 3,009 m
2. En el triángulo ABC de la figura 2, definido por un cateto b = 6 m., y el ángulo B = 49º, determinar los restantes elementos:
El ángulo C será: C = 90º - B = 90º - 49º = 41º
La hipotenusa a será: a = b / sen B = 6 / sen 49º = 6 / 0,75471 = 7,950 m
El cateto c será: c = b / tg B = 6 / tg 49º = 6 / 1,15037 = 5,216 m
3. En el triángulo ABC de la figura 2, definido por la hipotenusa a = 8 m, y el cateto c = 5 m, determinar los siguientes elementos:
El cateto b será: b2
= a2 - c2 = 82 - 52
=39 ; b = ![]() = 6,245 m
= 6,245 m
El ángulo B será: cos B = c / a = 5 / 8 = 0,625 ; B = 51º 19' 4''
El ángulo C será: sen C = c / a = 5 / 8 = 0,625 ; C = 38º 40' 56''
4. En el triángulo ABC de la figura 2, definido por los dos catetos b = 9 m, y c = 12 m, determinar los restantes elementos.
La hipotenusa a será: a2
= b2 + c2 = 92 + 122
= 225 ; a = ![]() = 15 m
= 15 m
El ángulo B será: tg B = b / c = 9 / 12 = 0,75 ; B = 36º 52' 12''
El ángulo C será: tg C = c / b = 12 / 9 = 1,3333 ; C = 53º 7' 48''
Ejercicios con triángulos rectangulos
| 1. | Un triángulo es tal que sus catetos miden 4 y 3 cm. Construirlo y calcular su hipotenusa y ángulos agudos. | 5 cm ; 53° 7' 48''; 36° 52' 12'' |
| 2. | Calcular el cateto c de un triángulo rectángulo, conocidos: B = 40°; b = 37m. | 44,09 m |
| 3. | Calcular el ángulo B de un triángulo rectángulo, conocidos la hipotenusa: a = 13 m, y un cateto: c = 6 m. | 62° 30' 49'' |
| 4. | Calcular el cateto b en un triángulo rectángulo del que se conocen: a = 7 m; C = 80°. | 1,216 m |
| 5. | Resolver el siguiente triángulo rectángulo: B = 37° 37'; c = 4 m |
C = 52º 23';
b = 3,08 a = 5,05 |
| 6. | Calcular el área de un triángulo rectángulo, conocidos la hipotenusa: a = 6 m, y un ángulo agudo: B = 38° 16'. | 8,753 m2 |
| 7. | Calcular el área de un triángulo rectángulo,
conocidos: b = 9,8 m; B = 26° 27'. |
96,52 m2 |
| 8. | Calcular el ángulo desigual de un triángulo isósceles, conocidos: a = 6 m; b = c = 4 m. | A = 97° 10' 51" |
| 9. | Calcular el área de un triángulo ABC, conocidos: B = C = 42°; a = 8 m. |
14,41 m2 |
| 10. | Calcular el perímetro de un octógono regular inscrito en una circunferencia de 6 m de radio. | 36,738 m |
| 11. | Calcular el lado de un decágono regular circunscrito a una circunferencia de 10 m de radio. | 6,498 m |
| 12. | Calcular el área de un dodecágono regular inscrito en una circunferencia de 2 m de radio. | 12 m |
| 13. | Una circunferencia tiene 4 m de radio. Calcular la cuerda que corresponde a un ángulo central de 68°. | 4,474 m |
| 14. | En una circunferencia de 8 m de radio, un ángulo
inscrito ABC, simétrico respecto del diámetro BD, mide 38° 40' 50'' . Calcular el área del triángulo ABC. |
71,22 m2 |
| 15. | Calcular la cuerda que corresponde a un ángulo
inscrito: µ = 60°, en una circunferencia de 7 m de radio. |
12,124 m |
| 16. | En una circunferencia de 10 m de diámetro, una cuerda mide 6 m. Calcular su distancia al centro de la circunferencia. | 4 m |
| 17. | Calcular el ángulo en el centro que corresponde a una cuerda de 10 m en una circunferencia de 6 m de radio. | 112° 53' 7" |
| 18. | Calcular la base menor de un trapecio rectángulo cuyos lados no paralelos miden 22 y 34 m, y cuya base mayor mide 40 m. | 14,08 m |
| 19. | Calcular la altura de una chimenea, sabiendo que la visual dirigida a su punto más alto por un observador forma un ángulo de 36° 40' con la horizontal. El observador, de 1,80 m de altura, se encuentra situado en el suelo, a 48 m de distancia del pie de la chimenea. | 37,535 m |
| 20. | Una escalera de 6,5 m de longitud se apoya en una pared, formando con ella un ángulo de 18°. Calcular la altura que alcanza. | 6,18 m |
| 23. | Una torre de 40 m de altura proyecta sobre el suelo una sombra de 16 m de longitud. ¿Qué sombra proyectara un árbol de 12 m de altura? | 4,8 m |
| 25. | Calcular la longitud de una correa plana que une exteriormente dos poleas de 24 y 12 cm de radios, cuyos centros se encuentran a 54 cm de distancia. | 223,78 cm |
| 26. | Calcula los ángulos de un trapecio isósceles sabiendo que la base mayor mide 60 cm., la menor 40 cm. y la altura 24 cm. ¿Cuánto miden los lados oblicuos?. | 67º 22' 48'
112º 37' 12' 26 cm |
| 27. | Halla el área de un pentágono regular inscrito en una circunferencia de 9 cm. de radio. | 192,56 cm2 |
| 28. | Halla los lados de un paralelogramo sabiendo que sus diagonales miden 5 y 11 cm.y el águlo que forman es de 23º. | 3,3 7,9 |
| 30. | Desde la orilla de un río se observa la copa de un árbol, que está situado en la otra orilla, bajo un ángulo de 60º . Si nos alejamos 8m. de la orilla, el ángulo de observación es de 45º. Calcula la altura del árbol y la anchura del río. | alt. = 18,93 anch=10,93 |
Resolución de triángulos oblicuángulos
| La suma de los ángulos de un triángulo
es igual a dos rectos. A + B + C = 180º |
|
Teorema del seno. En todo triángulo, la relación de un lado al seno del ángulo opuesto es constante.
![]()
Teorema del coseno. En todo triángulo, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados, menos dos veces el producto de esos lados multiplicado por el coseno del ángulo que comprenden.
b2 = a2 + c2
- 2ac · cos B
a2 = b2 + c2 - 2bc · cos A
c2 = a2 + b2 - 2ab · cos C
Ejercicios con triángulos oblicuángulos
| 1. | Calcular el lado b de un triángulo definido por a = 5m; B = 60º 10'; C = 30º 30' |
4,338 m |
| 2. | Calcular el ángulo A de un triángulo del que se
conocen a = 7m; b = 8m; c = 9 m |
48º 11' 23'' |
| 3. | Calcular el lado c de un triángulo definido por a = 17m; b = 10m; C = 37º |
10,84 m |
| 4. | Calcular el ángulo B de un triángulo definido por a = 1,8m; b = 5m; A = 21º |
84º 32' 32'' |
| 5. | Calcular el área de los siguientes triángulos a) b = 3,2m; c = 5,6m; A = 45º 40' b) a = 11,2m; B = 40º 40'; C = 36º c) a = 2m; b = 3,8m; c = 4,5m |
a) 6,409 m2 b) 24,69 m2 c) 3,773 m2 |
| 6. | Calcular el área de un rombo circunscrito a una circunferencia de 8m de radio, sabiendo que uno de sus ángulos es de 40º | 398,3 m2 |
| 7. | Hallar las diagonales de un paralelogramo, sabiendo que sus lados miden 6 y 8 metros y uno de sus ángulos 52º | 12,61 m, 6,4 m |
© Roberto de Diego
![]()