 |
Aritmética |
Los números naturales y sus operaciones
Al conjunto de los números naturales se le representa por la letra N y es el siguiente:
N = {0,1,2,3,4,.....,10,11,.......,100,101,.........}
Propiedades de la suma y la multiplicación
| PROPIEDAD | SUMA | MULTIPLICACIÓN |
| Asociativa | ( a + b ) + c = a + ( b + c ) | ( a · b ) · c = a · ( b · c ) |
| Conmutativa | a + b = b + a | a · b = b · a |
| Existencia de elemento neutro | Es el 0, puesto que a + 0 = a | Es el 1, puesto que a · 1 = a |
| Distributiva del producto respecto de la suma | a · ( b + c ) = a · b + a · c | |
Ejemplos
1. Propiedad asociativa y conmutativa:
40 + 19 + 60 = (40 + 60) + 19 = 100 + 19 = 119
2. La propiedad distributiva permite:
 | Sacar factor común: 24 · 3 + 24 · 5 + 24 · 2 = 24 · (3 + 5 + 2) = 24 · 10 = 240 |
| Agrupar términos semejantes: 2a + 3b + 5b + a = (2 + 1)· a + (3 + 5) · b = 3a + 8b |
| Deshacer paréntesis: 4 · (5 + 3x + 2x2) = 4 · 5 + 4 · 3x + 4 · 2x2 = 20 + 12x + 8x2 |
Las otras operaciones
Resta: La resta de dos números a y b, escrita a-b consiste en encontrar otro que sumado con b nos de a. Al numero a se le llama minuendo y a b sustraendo.
División: La división de un número D (dividendo) entre un número d (divisor), escrito D:d, consiste en calcular otro número c (cociente) tal que multiplicado por d nos de D.
Cuando la división no es exacta se obtiene un resto que sumado a la multiplicación de c·d nos da D.
Ejemplo
1. Efectuar la división: 135:8
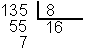
se tiene que : 135 = 8 · 16 + 7
Operaciones compuestas
1º. Si en una expresión figuran sumas, restas, multiplicaciones y divisiones (sin paréntesis), se efectúa en primer lugar las multiplicaciones y divisiones, comenzando de izquierda a derecha; y a continuación las sumas y restas.
2º Si en una expresión con números figura un paréntesis, se efectúa en primer lugar el paréntesis.
Potenciación y radicación
La potencia natural de un número natural no es más que una multiplicación reiterada.
an = a · a · a................n veces siendo a y n números naturales
Al número a se le llama base y al n exponente.
1º La multiplicación de potencias de la misma base es otra potencia de la misma base y cuyo exponente es la suma de los exponentes
am · an = am+n
2º. La multiplicación de potencias con el mismo exponente es otra potencia de igual exponente y cuya base es la multiplicación de las bases.
an · bn = (a · b)n
3º. La potencia de una potenciación es otra potencia de igual base y cuyo exponente es la multiplicación de los exponentes.
(am)n= am·n
4º. La potencia "0" de cualquier número es 1.
a0 = 1
La radicación es la operación inversa de la potenciación. En concreto encontrar la raíz n-ésima de un número consiste en encontrar otro que elevado a n nos dé el número original.
Ejercicios con números naturales
| 1. | Efectúa las siguientes operaciones: a) (8 + 3 + 6) - (5 + 4 + 3) b) 30 + [12 - (4 + 6)] c) 67 + [(9 - 1)+(4 - 3)+(7 - 5)] d) 26 +{7 - 2+[7 -(5 + 3 - 4)]} e) 37 - {5 +[(12 - 4)-(8 - 3)+(5 - 2)]} f) 47 - [(5 + 3)-(4 - 2)+ 3]+{12 -[(5 + 1)-(9 - 7)]} g) (8 - 6) · 3 + 2 · (5 - 2)+(7 - 3) · 4 - 3·(12 - 9) h) (5 · 4 · 8 · 7) · 3 i) (10 - 7) · 4 - 3 · (5 + 3)+ 7 · (6 - 4) j) 5 · [4 +(7 - 3) · 3 ] k) 8 · [(11 - 6) · 3 +(23 - 18) · 4] l) (7 · 6) · 8 + (4 · 2) · 3 m) 12 · 5 - 8 · 7 + 16 · 9 n) (8 - 4) : 2 + (16 - 4) : 3 - (18 : 6) ñ) (6 + 4) : 2 +(12 + 4) : 4 o) (4 · 3) : 2 +(17 + 3) : (2 + 3) p) 40 : [(6 - 4) · (4 - 2)] q) 45 : 5 - 8 : 4 + 18 : 9 r) 81 : 9 + 6 - 3 · 3 + 4 : 2 |
a) 5 b) 32 c) 78 d) 34 e) 26 f) 46 g) 19 h) 3.360 i) 2 j) 80 k) 280 l) 360 m)148 n) 3 ñ) 9 o) 10 p) 10 q) 9 r)8 |
| 2. | Un surtidor consume 470 litros de agua cada hora. Si cada día funciona durante 14 horas, ¿cuál es el consumo semanal del agua del surtidor? | 46.060 litros |
| 3. | Cada día que Luis sabe la lección el profesor le suma 10 puntos y cada día que no sabe le resta 5 puntos. Después de 20 días Luis tenía 80 puntos. ¿Cuántos días supo la lección y cuántos no la supo? | 12 días si 8 días no |
| 4. | Expresa como una sola potencia las siguientes
multiplicaciones: a) 52 · 53 · 55 b) x4 · x3 · x · x12 c) 3x · 3x · 3x · 3x |
a) 510 b) x20 c) 34x |
| 5. | Calcula: a) 24 · 34 · 54 b) an · bn · 2n |
a) 304 b) (2ab)n |
| 6. | Quita paréntesis y reduce: a) ( x2 y3 )5 b) ( 5a2b3 )2 c) ( x2 )2 · ( x3 )3 · x d) ( a2 )3 · b · a4 · ( b4 )2 e) [( 32 )3 ]5 |
a) x10 y15 b) 25a4b6 c) x14 d) a10b9 e) 330 |
|
|
Múltiplos y divisores
Se dice que un número es primo cuando tan solo es divisible por la unidad y por sí mismo.
Por el contrario, se dice que un número es compuesto cuando no es primo, es decir, cuando es divisible por otros números además de la unidad y de sí mismo.
Se dice que un número "a" es múltiplo de otro "b" cuando "a" se obtiene multiplicando "b" por cualquier numero natural. Así tenemos que 30 es múltiplo de 6 ya que 6 · 5 = 30.
Se dice que un número "a" es divisor de otro "b" cuando "a" esta contenido en "b" un número exactod e veces.
Descomposición en factores primos
Descomponer un número en factores primos consiste en expresarlo como un producto de números primos.
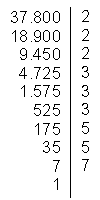Por lo tanto tendremos que
37.800 = 23 · 33 · 52 · 7
Máximo común divisor
Máximo común divisor de varios números es el mayor número que los divide a todos (m.c.d)
Para calcular el m.c.d. de varios números por el método de descomposición en factores primos, se descomponen en primer lugar todos los números en sus factores primos. Una vez efectuada la descomposición , el m.c.d. es igual al producto de todos los factores primos comunes con su menor exponente.
Ejemplo
Hallar el máximo común divisor de 1.680, 1.920, 14.520, 18.270:
Tenemos que :
1.680 = 24 · 3 · 5 · 7
1.920 = 27 · 3 · 5
14.520 = 23 · 3 · 5 · 112
18.270 = 2 · 32 · 5 · 7 · 29
Los factores comunes son 2, 3 y 5. Los menores exponentes con respectivamente, 1, 1, y 1. Por consiguiente el m.c.d. será 21 · 31 · 51 = 2 · 3 · 5 = 30.
Mínimo común múltiplo
Mínimo común múltiplo de varios números es el menor número que los contiene a todos un número exacto de veces (m.c.m).
Para calcular el m.c.m. de varios números por el método de descomposición en factores primos, se descomponen en primer lugar todos los números en sus factores primos, y el m.c.m. se obtiene como el producto de todos los factores primos comunes y no comunes con el mayor exponente.
Ejemplo:
Hallar el mínimo común múltiplo de 30, 32, 48 y 75
Tenemos que :
30 = 2 · 3 · 5
32 = 25
48 = 24 · 3
75 = 3 · 52
Por lo tanto el m.c.m es 25 · 3 · 52 = 2.400
Ejercicios con múltiplos y divisores
| 1. | Descomponer en factores primos a) 225 b) 686 c) 2.431 d) 7.350 e) 20.328 f) 425 |
a) 32 · 52 b) 2 · 73 c) 11 · 13 · 17 d) 2 · 3 · 52 · 72 e) 23 · 3 · 7 · 112 f) 52 · 17 |
| 2. | Hallar el máximo común divisor de : a) 432 y 1.560 b) 1.380 y 3.400 c) 66, 154 y 242 d) 1.275, 2.400 y 2.850 |
a) 24 b) 20 c) 22 d) 75 |
| 3. | Se tienen tres cajas que contienen 4.800, 6.000 y 10.176 kilos de jabón. El jabón de cada caja esta dividido en bloques del mismo peso, que es el mayor posible. ¿Cuanto pesa cada bloque y cuantos bloques hay en cada caja? | 48 kilos, 100 bloques en la primera, 375 en la segunda y 636 en la tercera |
| 4. | ¿Cual es la mayor longitud de una regla con la que se puede medir exactamente el largo y el ancho de una sala que tiene 2.550 cm. de largo y 1.785 cm de ancho? | 255 cm |
| 5. | Hallar el mínimo común múltiplo de: a) 36, 48 y 80 b) 96, 144 y 324 c) 8, 12, 24, 48 y 200 d) 70, 190, 280, 570 |
a) 720 b) 2.592 c) 1.200 d) 15.960 |
|
|
Los números enteros y sus operaciones
El conjunto de los números enteros se representa por Z y está formado por los naturales y sus "negativos". Es decir:
Z = { ..., -4, -3, -2, -1, 0, 1, 2, 3, 4,......}
Operaciones con números enteros
| PROPIEDAD | SUMA | MULTIPLICACIÓN |
| Asociativa | ( a + b ) + c = a + ( b + c ) | ( a · b ) · c = a · ( b · c ) |
| Conmutativa | a + b = b + a | a · b = b · a |
| Existencia de elemento neutro | Es el 0, puesto que a + 0 = a | Es el 1, puesto que a · 1 = a |
| Elemento simétrico | El opuesto de a es -a
porque a + (-a) = 0 |
No tiene |
| Distributiva del producto respecto de la suma | a · ( b + c ) = a · b + a · c | |
Algunas reglas para operar con números negativos son las siguientes:
1º. Si en una expresión figuran sumas de varios números positivos y negativos, se puede operar de dos modos:
|
Ejemplo:
Calcula la operación: 3 - 2 - ( -8) + 4 - 10 - 6
Solución: 3 - 2 - ( -8) + 4 - 10 - 6 = 3 - 2 + 8 + 4
- 10 - 6 = 9 + 4 - 10 - 6 = 3 - 6 = -3
2º. Si un paréntesis va precedido del signo menos, puedes suprimirlo de dos maneras:
|
Ejemplo:
Calcula la operación: -2 + 8 -(4 - 13 + 6 )
Solución: -2 + 8 -(4 - 13 + 6 ) = -2 + 8 - 4 + 13 - 6
= (8 + 13) - (2 + 4 + 6) = 21 - 12 = 9
3º. Para multiplicar números enteros se utiliza la llamada regla de los signos:
+ · + = + + · - = - - · + = - - · - = +
Potenciación y radicación
Para elevar números negativos a potencias naturales se opera de igual modo que para los números naturales
(- a) n = (-a) · (-a) · (-a)................n veces
Por lo tanto si tenemos en cuenta la paridad del exponente, se tendrá:
No hay que confundir ( -a)n y -an , la primera nos pide que multipliquemos -a por si mismo n veces, la segunda pide el opuesto del resultado de multiplicar a por si mismo n veces.
A los números enteros negativos sólo se le pueden extraer raíces de índice impar. Las de índice par no tienen sentido.
En efecto, podemos calcular 
, puesto que (-2)3 = -8, pero si intentamos calcular 
nos encontramos con que no existe ningún
numero que elevado al cuadrado nos de -16.
Ejercicios con números enteros
| 1. | Calcular el valor de las siguientes operaciones: a) 23 - 5 · (4 - 7) + 6 · (2 - 5) b) 22 - 4 · (9 - 3 · 2) c) 8 - [6 - (-3 + 7) - 6] + 4 d) (4 - 2) · 3 - 2 + 5 · (1 - 3) + 1 e) 7 -[3 + (8 + 5) · (3 - 1) + 5] f) 3 · 8 - 1 -[2 - 1 + (2 - 3) · 4 : 2] g) 6 - 5 · [-(-1) - 2 · 3 + 4 · (-6 + 8)] |
a) 20 b) 38 c) 8 d) -5 e) -27 f) 24 g) -9 |
| 2. | Expresar cono una sola potencia: a) (-2)4 · (-2)3 · (-2)6 · (-2) b) 33 · (-3)2 · 34 c) a2 · a3 · a8 |
a) 214 b) 39 c)a13 |
| 3. | Desarrolla las expresiones: a) (2 · 32 · 53)2 b) (4 · (-1)3 · (-3)2)3 c) (-2a3b5c)4 |
a) 22 · 34
· 56 b) -43 · 36 c) 16a12b20c4 |
|
|
Los números racionales y sus operaciones
Cuando las divisiones entre números enteros no es un número entero se necesita un conjunto mayor de números donde tenga cabida la división. Este conjunto es el de los números racionales. Las fracciones son las expresiones numéricas de los números racionales.
En estas fracciones el número encima de la línea se le llama numerador y el de abajo denominador
Todo entero es racional y por tanto los números fraccionarios complementan a los enteros dando lugar al conjunto de los números racionales. Se representa por la letra Q.
Simplificación de fracciones
| Se puede formar una fracción equivalente a |
|
|
Ejemplo: Simplificar la fracción 15 / 25
Si dividimos ambos términos por 3 obtenemos 3 / 5 que es una fracción irreductible.
Las fracciones con términos grandes pueden simplificarse más cómodamente dividiendo ambos términos entre su máximo común divisor.
Operaciones con números racionales
| Para sumar fracciones con el mismo denominador se suman los numeradores y se mantiene el denominador. |
| Para sumar fracciones con distinto denominador tendremos que transformarlas en otras equivalentes con el mismo denominador. |
Ejemplo
| 1º. Calcular: |
 |
Solución: |
 |
| 2º.Calcular: |
 |
| Solución: |
 |
Si algún sumando es un entero se le coloca 1 como denominador y se opera igual.
| El producto de dos fracciones es otra fracción cuyo denominador es el producto de sus denominadores y cuyo numerador es el producto de sus numeradores. |
| La división de dos fracciones es la multiplicación de la primera por la inversa de la segunda. |
| Potencias de fracciones |
 |
 |
 |
 |
 |
 |
Ejercicios con fracciones
| 1. | Reduce a común denominador las fracciones: a) 3 / 2, 6 / 3, 7 / 4 b) -7 / 12, 1 / 8, -3 / 4, 3 |
a) 18 / 12, 24 /
12, 21 / 12 b)-14 / 24, 3 / 24, -18 / 24, 72 / 24 |
| 2. | Reduce a fracción irreductible a) 12 / 18 b) -36 / 96 c) 1050 / 3500 d) 23 · 52 · 7 / 2 · 44 · 7 |
a) 2 / 3 b) -3 / 8 c) 3 / 10 d) 2 / 25 |
| 3. |  |
a) 19 /80 b) 17 / 36 c) -19 / 12 d) 94 / 15 |
| 4. | Calcula las siguientes potencias a) (-3)-2 b) (3 / 2)-3 c) (1 / 10)-1 |
a) 1 / 9 b) 8 / 27 c) 10 |
| 5. | Reduce a una sola potencia: |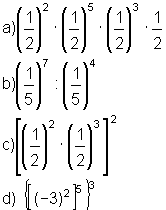
a) (1 / 2)11 b) (1 / 5)3 c) (1 / 2)10 d) 330 |
| 6. |  |
-11 |
|
|
Números decimales
Fracciones decimales son aquellas fracciones cuyo denominador es la unidad seguida de ceros.
Para escribir estas fracciones en notación decimal:
39 / 100 = 0,39 ; 7 / 1.000 = 0,007 ; 1.315 / 10.000 = 0,1315
Para convertir fracciones en números decimales se divide el numerador entre el denominador hasta que el cociente sea un numero exacto o bien hasta que se repita indefinidamente en el cociente una cifra o un grupo de cifras.
Cuando en el cociente haya un numero exacto tendremos un fracción decimal exacta: 0,125; 0,84.
Cuando en el cociente se repite un grupo de cifras en el mismo orden de modo indefinido a este grupo se le llama periodo.
Se dice que una fracción decimal es periódica pura cuando el período empieza en las décimas: 0,121212; 0,33333
Se dice que una fracción decimal es periódica mixta cuando el periodo no empieza en las décimas: 0,1477777; 0,12548484848; 0,21584777777
Conversión de números decimales en fracciones
La fracción irreductible que equivale a un número decimal dado recibe el nombre de fracción generatriz del número decimal.
Para hallar la fracción generatriz de una fracción decimal exacta se pone como numerador la fracción decimal sin la coma y como denominador la unidad seguida de tantos ceros como cifras decimales haya.
0,375 = 375 / 1000 que reduciendo se queda en 3 / 8
Para hallar la fracción generatriz de una fracción periódica pura se pone como numerador el periodo y como denominador tantos nueves como cifras tenga en periodo.
0,231231... ------> 231 / 999 que simplificando nos queda 77 / 333
Para hallar la fracción generatriz de una fracción periódica mixta se pone como numerador la diferencia entre la parte no periódica seguida del periodo y la parte no periódica, y como denominador tantos nueves como cifras tenga el periodo y tantos ceros como cifras tenga la parte no periódica.
0,49571571....... ----------> 49522 / 99900 que reduciendo nos queda 24.761 / 49.950
Ejercicios con números decimales
| 1. | El señor Martínez se ha comprado unos pantalones, una camisa, unos guantes y unos calcetines. Los calcetines le han costado 4,85, los guantes le han costado el doble que los calcetines, la camisa le ha costado 2,85 más que los guantes, y los pantalones el doble que la camisa. ¿Cuánto dinero ha gastado en total? | 52,2 |
| 2. | Un comerciante hace un pedido de 650 kg de mercancías y se lo envían en cuatro partidas. En la primera le mandan 82,54 kg; en la segunda 51 kg más que en la primera; en la tercera tanto como en las dos primeras juntas y en la cuarta le enviaron el resto. ¿Cuántos kg le enviaron en la última partida? | 217,84 |
| 3. | Juan compró una docena de bolígrafos a 2,60 pts. cada bolígrafo. Al comprar una docena le regalan otro bolígrafo igual. ¿A cuánto le resultó cada bolígrafo? | 2,4 |
| 4. | Enrique gana mensualmente $450 y ahorra cierta cantidad cada mes. Después de ganar $2.250 ha conseguido ahorrar $112,50. ¿Qué cantidad ahorra mensualmente? | 22,5 |
| 5. | Un comerciante compró 80 libros por $125. Vendió la cuarta parte a $1,50 cada libro, la mitad a $2,50 cada libro y el resto a $1,80 cada libro. ¿Qué beneficio obtuvo? | 41 |
| 6. | Un granjero compró 5 patos y 4 gallinas por $24,40. Más tarde compró 9 patos y 11 gallinas por $50,95 al mismo precio. Hallar el precio de un pato y de una gallina. | 3,40 un pato 1,85 una gallina |
| 7. | Un capataz contrata a un obrero para 30 días ofreciéndole $12,50 por cada día que trabaje y $6,20 por cada día que no trabaje. Al cabo de los 30 días el obrero recibió $299,40. ¿Cuántos días trabajó y cuántos días no trabajó? | 18 trabajo 12 no trabajo |
| 8. | ¿Qué número sumado con su triple da como resultado 4,70? | 1,175 |
| 9. | Un comerciante compró 120 cajas de cigarrillos por $300. Vendió 1.200 cigarrillos por $120 obteniendo un beneficio de $0,05 en cada cigarrillo. ¿Cuántos cigarrillos compró en total y cuántos había en cada caja? | 6.000 cigarrillos 50 en cada caja |
| 10. | Hallar la fracción generatriz de los números a) 0,053 b) 0,37 c) 0,0019 d) 0,000009 e) 1,6363 f) 3,254636363.... |
a) 53 / 1.000 b) 37 / 100 c) 19 / 10.000 d) 9 / 1.000.000 e) 18 / 11 f) 35.801 / 11.000 |
|
|
Regla de tres
La regla de tres es la operaciòn aritmetica que consiste en determinar el cuarto término de una proporción conocidos los otros tres.
Se dice que la regla de tres es simple cuando en ella intervienen dos magnitudes. Por el contrario, si en ella intervienen tres o más magnitudes se dice que la regla de tres es compuesta.
Resolución de reglas de tres simples.
Ejemplos
1. Si 10 pantalones cuestan 12.500, ¿Cuánto cuestan 15
pantalones?
Tendremos:
Supuesto
10 pantalones ----------> 12.500
Pregunta 15 pantalones
----------> x
Como puede observarse, el número de pantalones y el coste son magnitudes directamente proporcionales puesto que a más pantalones más dinero y a menos pantalones menos dinero. Por consiguiente podemos establecer la siguiente proporción:
 |
; |  |
2. Si 6 obreros hacen una obre en 8 dias, ¿En cuantos
días harán la misma obra 4 obreros?
Tendremos:
Supuesto
6 obreros --------> 8 días
Pregunta 4 obreros ------>
x
Como puede observarse, el número de obreros y el tiempo empleado en hacer la obra son magnitudes inversamente proporcionales entre sí puesto que a más obreros menos tiempo y a menos obreros más tiempo. Por consiguiente podemos establecer la siguiente proporción:
 |
; |
|
Ejerciciós con reglas de tres
| 1. | Un edificio de 20 metros de altura produce una sombra de 30 metros. ¿Cuál será la estatura de una persona que a la misma hora produce una sombra de 2,70 metros? | 1,80 |
| 2. | Los 2 / 3 de la capacidad de un depósito son 60 litros. ¿Cuál será la capacidad de los 5 / 6 del mismo depósito? | 75 |
| 3. | Un grupo formado por 9 obreros puede hacer una obra en 6 dias. ¿Cuántos obreros se necesitarán para hacer la misma obra en 3 dias? | 18 |
| 4. | Un automóvil que lleva una velocidad de 60 km/h tarda 4 horas en recorrer el trayecto entre dos ciudades. ¿Cuánto tiempo hubiera tardado si su velocidad hubiera sido de 80 km/h? | 3 |
| 5. | Una calle que mide 25 m de largo y 4 m de ancho está pavimentada por 16.000 adoquines. ¿Cuántos adoquines se necesitarán para pavimentar otra calle de 30 m de largo y 5 m de ancho? | 24.000 |
| 6. | Dos obreros deben repartirse 30.000 pesos que han cobrado por un trabajo realizado conjuntamente. Si el primero trabajó 12 dias a razón de 8 horas diarias y recibió 20.000 pesos, ¿cuántos dias a razón de 6 horas diarias trabajó el segundo? | 8 |
| 7. | Una finca pertenece a dos socios. El primero posee los 5 / 9 de la finca y su parte está valorada en $9.000. ¿En cuánto está valorada la parte del otro socio? | 7.200 |
| 8. | Un caminante recorre 9 km en 10 minutos. ¿Cuánto tiempo tardará en recorrer 27 km? | 30 |
| 9. | Un grupo de 18 obreros puede hacer una obra en 12 días. ¿Cuantos obreros serían necesarios para efectuar la misma obra en 27 días? | 8 |
|
|
Raices
Las radicación es la operación inversa de la potenciación y consiste en hallar la base conocidos el exponente y la potencia.
Asi si tenemos que 72 = 49, podemos escribir
que 
,
donde el signo 
es el
signo radical, 49 es la cantidad subradical, 7
es la raíz cuadrada y el número 2 es indice de la raíz. Es
este caso al ser el indice 2 la raiz es cuadrada, si
fuera 3 seria raiz cubica, 4 raiz cuarte,
ect. Cuando el indice es 2 usualmente se omite.
Propiedades
1º. Si a los dos miembros de una igualdad se les extrae la misma raíz se obtiene otra igualdad.
2º. La raiz enesima de un producto de varios factores es igual al producto de las raíces enésimas de cada uno de los factores.
3º. La raíz enésima de una fracción es igual a la raíz enésima del númerador dividida por la raíz enésima del denominador.
4º. La raíz enésima de una potencia se obtiene dividiendo el exponente de la potencia por el indice de la raíz.
5º. Para elevar un radical a una potencia se eleva la cantidad subradical a dicha potencia.
6º. La raíz enésima de una raíz se obtiene multiplicando los índices de ambas raíces.
Extracción de raices cuadradas.
Para hallar la raíz cuadrada de un número entero se van separando grupos o períodos de dos cifras del número dado, empezando por la derecha. A continuación se extrae la raíz cuadrada del primer periodo que haya quedado a la izquierda y ésta será la primera cifra de la raíz cuadrada. Seguidamente se eleva dicha cifra al cuadrado y el resultado obtenido se resta del primer periodo. A la derecha del resto obtenido se sitúa el siguiente periodo. A continuación se separa la primera cifra de la derecha con una coma y se divide el número que queda a la izquierda por el doble de la raíz hallada. El cociente obtenido será o bien la cifra siguiente de la raíz cuadrada o bien una cifra mayor.
| Para comprobarlo se escribe dicha cifra a la derecha del doble de la raíz hallada y el número resultante se multiplica por la cifra que se comprueba. Si el producto obtenido se puede restar del número que resulta al separar la primera cifra de la derecha se sube la cifra a la raíz. Si no se puede restar se disminuye la cifra en una unidad o en las que sean necesarias para que el producto se pueda restar. Una vez efectuada esta operación se resta el producto obtenido y a la derecha del resto se coloca el siguiente periodo, repitiéndose las operaciones indicadas anteriormente hasta que se haya bajado el último periodo. |
 |
Así pues, 4.623 es la
raíz cuadrada por defecto de 21.378.948
y 6.819 es el resto.
Comprobemosque el resultado obtenido es correcto:
4.6232 + 6.819 = 21.372.129 + 6.819 = 21.378.948,
Lo cual indica que el resultado obtenido es correcto.
Para hallar la raíz cuadrada de un número decimal se separa el número decimal en períodos de dos cifras a derecha e izquierda de la coma decimal añadiendo un cero al último período de la derecha si quedara con una sola cifra decimal. A continuación se extrae la raíz cuadrada como si se tratara de un número entero poniendo la coma decimal en la raíz al bajar el primer período decimal.
Ejercicios con raices
| 1. | Expresar en forma exponencial |
a) x1/5 b) (x2/3)5 c) a6/15 d) (a13/a6)1/2 e) (ak/m)1/n |
| 2. | Calcula las siguientes potencias a) 1251/3 b) 82/3 c) 645/6 |
a) 5 b) 4 c)32 |
| 3. | Expresar en forma radical a) x7/9 b) (m5 · n5)1/3 c) a1/2 · b1/3 |
 |
| 4. | Hallar la raíz cuadrada de a) 15217801 b) 1492,2769 c) 7100,421696 |
a) 3901 b) 38,63 c) 84,264 |
© Roberto de Diego
