Algebra

1.	Resolver las siguientes ecuaciones a) 3x + 11 = 8x + 6 b) 4x + 10 = 7x + 4 c) 6 - 2x = 3x - 4 d) 12 - 2x = x - 3 e) x / 2 + x / 3 = 5 f) x / 5 + x / 8 = 15 - x / 20 g) x / 4 + x / 6 = x / 8 + 14 h) (x - 2) / 3 - (x - 4) / 5 = (x - 6) / 7	a) x = 1 b) x = 2 c) x = 2 d) x = 5 e) x = 6 f) x = 40 g) x = 48 h) x = 104
2.	Resolver las ecuaciones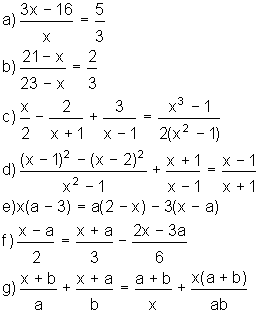	a) x = 12 b) x = 17 c) x = -11 d) x = 1 / 2 e) x = 5 / 2 f) x = 8a / 3 g) x = (a²b + ab²) / (a² + b²)
3.	Se ha vendido 1/3, 1/4 y 1/6 de una pieza de tela y todavía quedan 36 metros. hallar la longitud de la pieza de tela.	144 metros
4.	La suma de dos números es 48. Si se les aumenta a los dos 16 unidades, su razón es 3/5. ¿Cuáles son estos números?	14 y 34
5.	Una persona ha comprado 1/5 y otra 2/3 de una pieza de tela. Si la segunda se lleva 42 metros más que la primera, ¿cuál era la longitud de la pieza de tela?	90 metros
6.	Una persona tiene actualmente 3 veces la edad de su sobrino. Dentro de 10 años su edad será únicamente el doble. Hallar la edad de cada uno.	30 y 10 años
7.	La suma de las edades de dos personas es actualmente de 84 años. Si 1/3 de la edad del más joven equivale a 1/4 de la edad del mayor, ¿cuál es la edad de cada uno?	36 y 48 años
8.	Un obrero debe terminar cierto número de metros de obra en 14 días. Trabajando 8 horas diarias le faltarían 8 metros y trabajando 9 horas diarias haría 6 metros más de lo convenido. ¿Cuántos metros tiene que hacer?	120 metros
10.	Un comerciante que ha vendido los 3/5 de una partida de manzanas dice que añadiendo 230 a las que quedan, la cantidad inicial de manzanas aumentaria en 1/6. ¿Cuántas manzanas habla al principio?	300
11.	Un viajero ha recorrido el primer día de su viaje 1/4 de su camino; el segundo día los 5/9 y el tercer día termina el viaje recorriendo 42 km. ¿Cuál es la longitud del recorrido?	216 km
12.	Un galgo persigue a una liebre que está a 60 metros de distancia. Si el galgo recorre 6 m/s y la liebre 4 m/s, ¿cuánto tardará el galgo en alcanzar a la liebre?	30 segundos
13.	La suma de dos números es 80 y el mayor excede al menor en 6. Hallar los números.	43 y 37
14.	Dividir 114 en tres partes tales que la segunda sea el doble de la primera y la suma de las dos primeras exceda a la tercera en 30.	24, 48, 42
15.	La edad de un padre es el triple que la de su hijo y hace 4 años era 4 veces la de su hijo. Hallar las edades actuales.	36 y 12 años
16.	Un comerciante adquiere 100 trajes y 70 pares de zapatos por 32.000 balboas. Cada traje costó el doble de lo que costó cada par de zapatos más 50 balboas. Hallar el precio de un traje y el de un par de zapatos.	250 el traje 100 los zapatos
17.	Seis personas iban a comprar una casa contribuyendo por partes iguales, pero dos de ellas desistieron del negocio y entonces cada una de las restantes tuvo que poner 4.000 bolívares más. ¿Cuál era el valor de la casa?	48.000 bolívares
18.	La suma de dos números es 58 y el doble del mayor excede al triple del menor en 11. Hallar los números.	37 y 21
19.	El largo de un barco, que es 133 metros, excede en 13 metros a 8 veces el ancho. Hallar el ancho del barco.	15 metros
20.	Un ganadero compró cuatro veces más caballos que vacas. Si hubiera comprado 2 caballos más y 2 vacas más tendría triple número de caballos que de vacas. ¿Cuántos caballos y cuántas vacas compró?	16 caballos 4 vacas
21.	En cada día de lunes a jueves, Juan ganó $10 más de lo que ganó el día anterior. Si el jueves ganó cuatro veces más que lo que ganó el lunes, ¿cuánto ganó cada día?	10 el lunes, 20 el martes, 30 el miércoles y 40 el jueves.
22.	Hace 4 años la edad de un padre era tres veces la de su hijo y dentro de 6 años será el doble. ¿Qué edades tienen ahora el padre y el hijo?	34 y 14 años
23.	Dentro de 2 años la edad de un padre será el triple que la de su hijo y hace 4 años era cinco veces la del hijo. Hallar las edades actuales.	34 y 10 años
24.	La edad de José es el triple que la de Roberto y ambas edades suman 60 años. Hallar ambas edades.	José 45 y Roberto 15
25.	El mayor de dos números es 6 veces el menor y ambos números suman 56.	48 y 8
26.	Repartir 700 balboas entre tres personas de modo que la parte de la segunda sea la mitad de la primera y un cuarto de la de la tercera.	200, 100, 400 respectivamente
27.	Dividir el número 200 en tres partes de modo que la primera sea el cuarto de la segunda y el quinto de la tercera.	20, 80, 100
28	Si un número se multiplica por 7 el resultado es el número aumentado en 24. Hallar el número.	4
29.	Si al triple de la edad de José le añadimos 15 años, tendría 90 años. ¿Qué edad tiene José?	25 años
30.	Dividir 136 en tres partes tales que la primera sea el triple de la segunda y la tercera igual a la suma de la primera y la segunda.	51, 17 y 68
31.	La edad de Eva es la mitad de la de Pilar; la de Juana el triple de la de Eva y la de Eugenia el doble que la de Juana. Si las cuatro edades suman 144 años, ¿qué edad tiene cada una?	Eva 12, Pilar 24, Juana 36 Eugenia 72
32.	Dividir 120 en dos partes tales que la mayor disminuida en 5 equivalga a la menor aumentada en 5.	65 y 55
33.	Entre Juan y José tienen 820 bolívares. Si Juan pierde 20, lo que le queda equivale a lo que tiene José. ¿Cuánto tiene cada uno?	420 Juan y 400 José
34.	Dos ángulos suman 90° y el doble del menor excede en 30° al mayor. Hallar los ángulos.	50º y 40º
35.	La suma de dos números es 72 y el mayor excede al triple del menor en 4. Hallar los números.	55 y 17
36.	La diferencia de dos números es 60. Si el mayor se disminuye en 10 se tiene el triple del menor. Hallar los números.	85 y 25
37.	Un perro y su collar han costado $80 y el perro costó 9 veces lo que el collar. ¿Cuánto costó el perro y cuánto el collar?	72 el perro y 8 el collar
38	Entre Pedro y Eduardo tienen $160. Si Pedro pierde $9 y Eduardo gana $5, ambos tienen lo mismo, ¿Cuánto tiene cada uno?	87 Pedro y 73 Eduardo
39	En una clase hay 50 alumnos entre niños y niñas. El número de niñas excede en 5 al doble de los niños. ¿Cuántos niños hay en la clase y cuántas niñas?	35 niñas y 15 niños
40	Dividir 32 en dos partes tales que el triple de la parte menor disminuido en la parte mayor equivalga a 16.	20 y 12

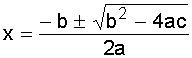
1.	Resolver la ecuación a) x² - 3x + 2 = 0. b) x²- 5x + 6 = 0. c) x² - 5x + 4 = 0. d) x² - 12x + 35 = 0. e) x² - 13x + 40 = 0. f) x² - 6x - 7 = 0. g) 2x² - 28x + 96 = 0. h) 3X² - 243 = 0. i) 5X² - 25x - 70 = 0. j) 4X² - 16 = 0. k) 5X² - 25x - 120 = 0. l) 5X² - 25x - 180 = 0. m) 2x² - 32 = 0. n) 4X² + 24x + 20 = 0.	a) x¹ = 1 ; x² = 2 b) x¹ = 2 ; x² = 3 c) x¹ = 4 ; x² = 1 d) x¹ = 7 ; x² = 5 e) x¹ = 8 ; x² = 5 f) x¹ = -1 ; x² = 7 g) x¹ = 8 ; x² = 6 h) x¹ = -9 ; x² = 9 i) x¹ = 7 ; x² = -2 j) x¹ = 2 ; x² = -2 k) x¹ = -3 ; x² = 8 l) x¹ = 9 ; x² = -4 m) x¹ = 4 ; x² = -4 n) x¹ = -5 ; x² = -1
2.	¿Cuál es el número positivo cuyos 4/5 multiplicados por los 3/4 dan 2.160?	60
3.	El producto de un número positivo aumentado en 15 por el mismo número disminuido en 15 da 99. ¿Cuál es el número?	18
4.	Hállese un número cuyo cuadrado le excede en 110 unidades.	11
5.	La diferencia de dos números es 5 y su suma multiplicada por el número menor equivale a 133. Hallar los números.	12 y 7
6.	Una compañía de 720 hombres está dispuesta en filas. El número de soldados de cada fila es 6 más que el número de filas que hay. ¿Cuántas filas hay y cuántos soldados en cada una?	24 filas 30 soldados por f.
7.	Juan compró cierto número de plumas por $32. Si cada pluma le hubiera costado $4 menos, podía haber comprado 4 plumas más por el mismo dinero. ¿Cuántas plumas compró y cuánto le costó cada pluma?	4 plumas $8.
8.	Un tren emplea cierto tiempo en recorrer 360 km. Si la velocidad hubiera sido 30 km/h más que la que llevaba hubiera tardado 2 horas menos en recorrer dicha distancia. ¿En qué tiempo recorrió los 360 km?	6 horas
9.	Un hombre compró cierto número de caballos por $3.600. Se le murieron 3 caballos y vendiendo cada uno de los restantes a $150 más de lo que le costó cada uno ganó en total $450. ¿Cuántos caballos compró y cuánto le costó cada uno?	12 caballos. $300.
10.	Hallar tres números enteros consecutivos tales que el cociente del mayor entre el menor equivalga a los 2/3 del número intermedio.	2, 3 y 4
11.	El producto de dos números es 48 y su cociente es 3. Hallar los números.	12 y 4
12.	El producto de dos números es 48 y si el mayor se divide por el menor el cociente es 1 y el resto 2. Hallar los números.	8 y 6
13.	Un tren ha recorrido 480 km en cierto tiempo. Para haber recorrido esa distancia en 2 horas menos, la velocidad debía haber sido 20 km/h más. Hallar la velocidad del tren.	60 km / h

Algebra

Resolución de ecuaciones de primer grado (Ejercicios)

Resolución de ecuaciones de 2º grado