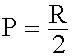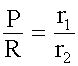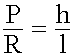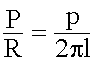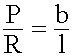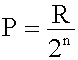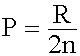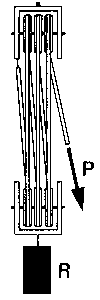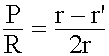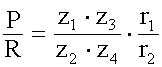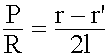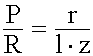| |
Máquinas |
Introducción
Máquinas son dispositivos destinados a vencer una fuerza, llamada "resistencia" , mediante la acción de otra, llamada "potencia".
Trabajo motor es el realizado por la potencia. Se representa por Wm.
Trabajo resistente es el trabajo realizado por la resistencia. Se representa por Wr.
Considerando que una máquina no puede crear trabajo, el trabajo resistente que la máquina nos devuelve ha de ser igual al trabajo motor que se le haya suministrado.
Wm = Wr
Ley de una máquina.- Es una fórmula matemática que relaciona el valor de la potencia con el de la resistencia.
Clasificación de las máquinas
| Máquinas simples.- Son las más sencillas. |
Máquinas compuestas.- Son las que están formadas por una combinación de máquinas simples.
- Combinación exponencial |
|
|
Máquinas simples
Palanca
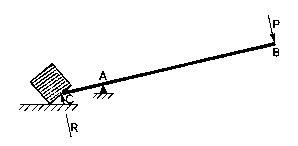
| Palanca es una máquina constituida por una barra rígida que puede girar alrededor de un punto y en la que se consideran los siguientes elementos: Punto de apoyo.- Punto A Brazo de potencia.- Distancia A - B Brazo de resistencia.- Distancia A - C |
 |
Ley de la palanca.- En toda palanca, el producto de la potencia (P)por su brazo (bP) es igual al producto de la resistencia (R) por el suyo (bR).
![]()
Ejemplo: Una palanca de 1,5 m de longitud se apoya de tal manera que
sus brazos de potencia y resistencia
son 1,3 y 0,2 m respectivamente. Calcular la resistencia que se puede vencer mediante una
potencia de 50 kgf.
P = 50 kgf ; bP = 1,3 m ; bR = 0,2 m
| P · bP = R · bR -----> 50 · 1,3 = R · 0,2 |
|
Géneros de palanca.-
| Palanca de primer genero es aquella en la que el punto de apoyo está situado entre la potencia y la resistencia. | 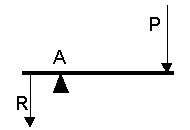 |
| Palanca de segundo genero es aquella en la que la resistencia actúa entre el punto de apoyo y la potencia. | 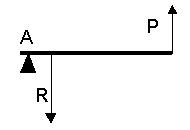 |
| Palanca de tercer genero es aquella en la que la potencia esta situada entre el punto de apoyo y la resistencia. | 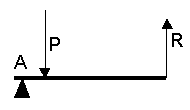 |
|
|
Polea fija
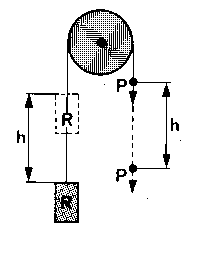
| Es una máquina constituida por un disco que puede girar sobre un eje fijo y tiene en su periferia un canal que aloja una cuerda.
En una polea fija la potencia es igual a la resistencia. |
 |
|
|
Polea móvil
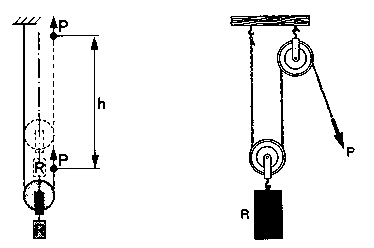
| Es una máquina análoga a la polea fija, con la única diferencia de que el eje de la polea puede moverse en sentido ascendente o descendente.
En una polea móvil la potencia es igual a la mitad de la resistencia.
|
 |
|
|
Torno
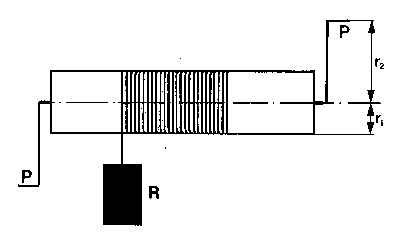
| Torno es una máquina constituida por un cilindro que lleva arrollada una cuerda y que puede girar sobre su eje mediante la acción de una manivela.
En un torno, la razón entre la potencia y la resistencia es igual a la razón entre los radios del cilindro y la manivela, respectivamente. |
 |
|
|
Plano inclinado
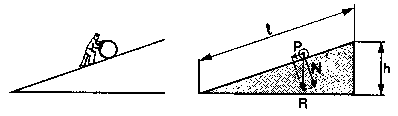
| Plano inclinado es una superficie plana que forma un ángulo con el suelo y se utiliza para elevar cuerpos.
En un plano inclinado, la razón entre la potencia y la resistencia es igual a la razón entre la altura y la longitud del plano inclinado. |
 |
|
|
Tornillo
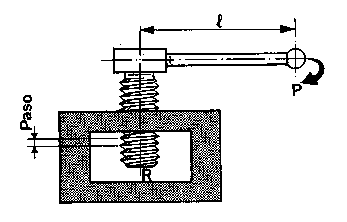
| El tornillo es una máquina constituida por una "cabeza", sobre la que se aplica la potencia, y una parte cilíndrica, sobre la que se ha tallado un surco de sección triangular o cuadrangular, que se denomina "rosca" y describe una espiral.
En un tornillo, la razón entre la potencia y la resistencia es igual a la razón entre el paso del tornillo y la longitud de la circunferencia descrita por el extremo de la llave. |
 |
|
|
Cuña
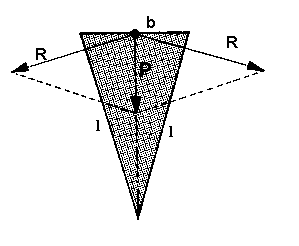
| La cuña es un prisma triangular construido con un material duro y tenaz, que se emplea para romper o separar cuerpos.
En una cuña, la razón entre la potencia y la resistencia es igual a la razón entre la cabeza y el lado de la cuña. |
 |
|
|
Ejercicios de máquinas simples
| 1. | Con una palanca de 2 m de longitud, apoyada a 15 cm de su extremo, se desea elevar un peso de 600 kgf. Calcular la fuerza que es necesario aplicar. | 48,6 kgf |
| 2. | Unas tenazas de cortar alambre tienen el filo a 3 cm de la bisagra. Calcular el esfuerzo de corte cuando se aplica sobre el mango una potencia de 50 kgf, sabiendo que éste tiene una longitud de 20 cm. | 333,3 kgf |
| 3. | Una persona pesa 80 kgf. Calcular el peso que puede elevar al colgarse del extremo libre de la cuerda de una polea móvil. | 160 kgf |
| 4. | Los radios del cilindro y de la manivela de un torno son 8 y 55 cm, respectivamente. Calcular el peso que se puede elevar ejerciendo una potencia de 10 kgf. | 68,75 kgf |
| 5. | Los radios del cilindro y de la manivela de un torno son 10 y 50 cm, respectivamente. Calcular -en kgm / s- la potencia desarrollada por una persona que, levantando un peso de 100 kgf, hace girar la manivela con una velocidad de 0,4 m/s. | 8 kgm / s |
| 6. | Un cuerpo se desliza, sin rozamiento, por un plano inclinado de 4 m de longitud y 2 m de desnivel. Calcular su aceleración. | 4,9 m / s2 |
| 7. | Calcular con qué fuerza es preciso empujar un cajón de 200 kgf de peso que se encuentra sobre un plano cuya pendiente es del 8 % (8 m de desnivel por cada 100 m de recorrido). | 16 kgf |
| 8. | Una carretera rectilínea tiene 2 km de longitud y 150 m de desnivel. Calcular con qué velocidad podrá subir por ella un coche de 350 kg. con una potencia de 7 CV. | 72 km / h |
| 9. | Calcular la fuerza de apriete de un tornillo de 12 mm de paso, cuando se ejerce sobre él una potencia de 8 kgf mediante una llave de 15 cm de longitud. | 628,3 kgf |
| 10. | Calcular el paso que deberá tener un tornillo para que con una potencia de 1,2 kgf, aplicada por medio de una llave de 20 cm de longitud, se consiga una fuerza de apriete de 100 kgf. | 15,1 mm |
| 11. | Calcular la fuerza de apriete de un grifo de 6 cm de diámetro y 0,8 mm de paso de rosca, cuando se ejerce con la mano una fuerza de 0,3 kgf. | 70,7 kgf |
| 12. | Con objeto de romper una roca, se coloca en una grieta una cuña de 25 cm de lado y 2 cm de cabeza. Calcular la resistencia que se puede vencer al golpear la cabeza de la cuña con una fuerza de 200 kgf. | 2.500 kgf |
|
|
Máquinas compuestas
Combinación exponencial
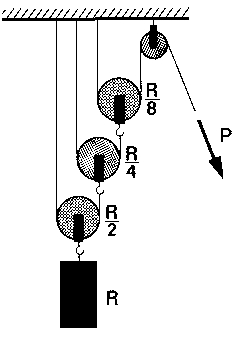
| Está constituida por varias poleas móviles agrupadas en la forma indicada en la figura.
En una combinación exponencial de "n" poleas móviles, la potencia es igual al cociente que resulta de dividir la resistencia entre 2n |
|
|
|
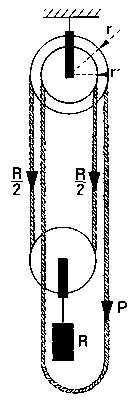
Combinación potencial o polipasto
| Consiste en un grupo de poleas fijas, colocadas sobre un eje común, y otro grupo formado por el mismo numero de poleas móviles, colocadas sobre otro eje paralelo al primero.
En una combinación potencial de "n" poleas móviles, la potencia es igual al cociente que resulta dividir la resistencia entre 2n. |
|
|
|
Polea diferencial
| Está constituida por dos poleas fijas de diferente radio, solidarias en un mismo eje, y una polea móvil de radio intermedio al de ambas.
En una polea diferencial, la razón entre la potencia y la resistencia es igual a la razón entre la diferencia de los radios de las poleas fijas y el duplo del radio de la mayor de ellas. |
|
|
|
Tren de engranajes
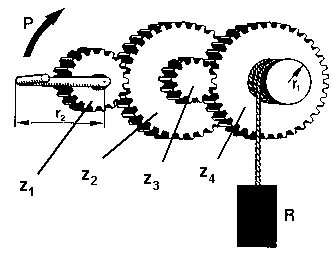
| Tren de engranajes es un mecanismo constituido por ruedas dentadas que se hayan engranadas entre si. Las ruedas que transmiten el movimiento se llaman "conductoras" y a las que se transmite el movimiento "conducidas". Siendo z1 y z3 el numero de dientes de las ruedas conductoras, z2 y z4 el numero de dientes de las ruedas conducidas, r2 radio de la manivela, r1 radio del tambor, la ley del tren de engranajes es.
|
|
|
|
Torno diferencial
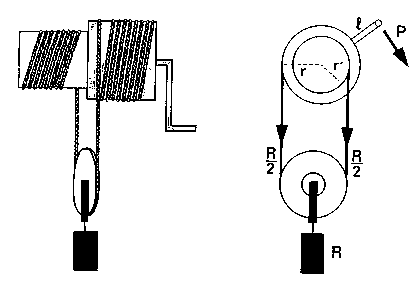
| Es una máquina consistente en dos cilindros, coaxiales y solidarios, de radios desiguales, a cada uno de los cuales y en diferente sentido va arrollado el extremo de una cuerda de la que cuelga una polea móvil.
En un torno diferencial, la razón entre la potencia y la resistencia es igual a la razón entre la diferencia de los radios de los cilindros y el duplo de la longitud de la manivela. |
 |
|
|
Tornillo sin fin
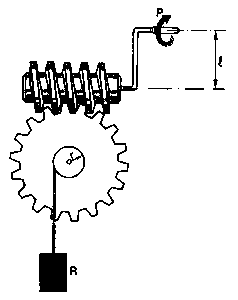
| Tornillo sin fin es una máquina compuesta resultante de la combinación de un tornillo y un torno.
En un tornillo sin fin, la razón entre la potencia y la resistencia es igual al cociente que resulta de dividir el radio del cilindro entre el producto de la longitud de la manivela por el numero de dientes de la rueda. |
|
|
|
Ejercicios de máquinas compuestas
| 1. | Calcular el menor número de poleas móviles que se deben colocar en una combinación exponencial, para que la potencia sea menor que la centésima parte de la resistencia. | 7 |
| 2. | Resolver el mismo problema anterior, para una combinación potencial de poleas. | 51 |
| 3. | Una combinación exponencial consta de 10 poleas móviles. Calcular el peso que puede elevarse con una potencia de 1 kgf. | 1024 kgf |
| 4. | Resolver el mismo problema anterior, para una combinación potencial de poleas. | 20 kgf |
| 5. | En una polea diferencial, los radios de las poleas fijas son 8,5 y 10 cm. Calcular la resistencia que es posible elevar con una potencia de 30 kgf. | 400 kgf |
| 6. | En una polea diferencial, la razón entre los radios de las dos poleas fijas es 1,1. ¿Cuál será la razón entre la resistencia y la potencia?. | 22 |
| 7. | En un tren de engranajes, las ruedas conductoras tienen 30 y 40 dientes, en tanto que las dos conducidas tienen 100 dientes. La última rueda conducida es coaxial y solidaria con un torno de 40 cm de diámetro. ¿Qué resistencia es posible vencer mediante una potencia de 12 kgf, aplicada con una manivela de 80 cm de radio?. | 400 kgf |
| 8. | En un tren de engranajes de cuatro ruedas, se sustituye
la segunda conducida por una cremallera de paso p, sobre la que actúa la resistencia
longitudinalmente. Deducir la ley de la maquina compuesta que resulta, considerando que
las ruedas conductoras tienen z1 y z3 dientes, que la conducida
tiene z2 dientes, y que la potencia se aplica sobre la primera rueda conductora
mediante una manivela de longitud " l ". |
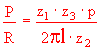 |
| 9. | Calcular el paso que deberá tener la cremallera de la maquina del ejercicio anterior, para que, siendo z1 = z3 = 20 y z2 = 1OO, la potencia, aplicada mediante una manivela de 40 cm de longitud, consiga vencer una resistencia 100 veces mayor. | 6,3 mm |
| 10. | En un torno diferencial, los radios de los cilindros son 20 y 9 cm, y el radio de la manivela 40 cm. Calcular la resistencia que se podrá vencer con una potencia de 100 kgf. | 727,3 kgf |
| 11. | En un torno diferencial, los radios de los cilindros son 11 y 9 cm. ¿Cuál deberá ser el radio de la manivela para que la razón entre la resistencia y la potencia sea 50?. | 50 cm |
| 12. | En un torno diferencial, los radios del cilindro mayor y de la manivela son 20 y 50 cm, respectivamente. ¿Cuál deberá ser el radio del cilindro menor, para que la relación entre la resistencia y la potencia sea 10?. | 10 cm |
| 13. | En un tornillo sin fin, los radios del torno y la manivela son 10 y 40 cm, respectivamente, y la rueda dentada tiene 80 dientes. Calcular la resistencia que es posible vencer mediante una potencia de 12 kgf. | 3840 kgf |
| 14. | Calcular el mínimo número de dientes que deberá tener la rueda engranada a un tornillo sin fin, cuyo cilindro tiene 8,2 cm de radio, para que con una potencia aplicada mediante una manivela de 30 cm de radio se consiga vencer una resistencia 100 veces mayor. | 28 |
| 15. | La longitud de la manivela de un tornillo sin fin es tres veces mayor que el radio del cilindro. ¿Cuál deberá ser el mínimo número de dientes de la rueda para que con una potencia de 7 kgf se consiga vencer una resistencia de 900 kgf?. | 43 |
© Roberto de Diego
![]()