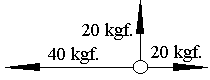Fuerzas

Estática

Estática es la parte de la Mecánica que estudia las fuerzas que actúan sobre los cuerpos en equilibrio.

Definición estatica de fuerza

Fuerza es toda acción capaz de deformar un cuerpo que se encuentra fijo.

Tipos de fuerza

Según su forma de actuación, las fuerzas pueden ser: de contacto y de acción a distancia.

Fuerzas de contacto.- Son aquellas que tienen lugar entre cuerpos que se tocan:

Fuerzas musculares: son las ejercidas por la acción muscular del hombre y los animales.

Fuerzas elasticas: son las ejercidas por resortes u otros cuerpos elásticos cuando se encuentran deformados.

Fuerzas de presión: son las ejercidas por los gases cuando se encuentran comprimidos.

Fuerzas de acción a distancia.- Son aquellas que tienen lugar entre dos cuerpos, sin necesidad de que haya contacto entre ellos:

Fuerzas gravitatorias: Son las fuerzas de atracción que tienen lugar entre los cuerpos.

Fuerzas eléctricas: Son las fuerzas de atracción y repulsión que tienen lugar entre cargas electricas.

Fuerzas magnéticas: Fuerzas ejercidas por los imanes.

Representación de las fuerzas

Para definir una fuerza es preciso enunciar cuatro caracteristicas:

Punto de aplicación.- Es el punto en el cual actua la fuerza.

Dirección.- Es la de la recta que contiene a la fuerza.

Sentido.- En cada dirección son posibles dos sentidos, correspondientes a cada una de las dos semirrectas existentes en dicha dirección.

Intensidad.- Intensidad o módulo es el valor numérico que expresa la cuantia de la fuerza.

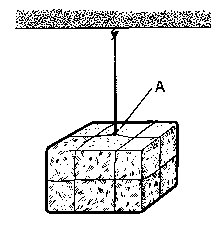Figura 1
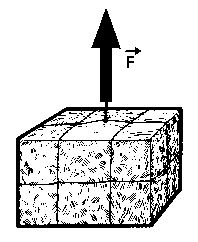Figura 2

La figura 1 representa un cuerpo suspendido de una cuerda. La cuerda ejerce sobre el cuerpo un fuerza cuyas caracteristicas son:

-Punto de aplicación: Es el punto donde la cuerda actua sobre el cuerpo, A.
-Dirección: Es la recta vertical que pasa por A.
-Sentido: Hacia arriba.
-Intensidad: Es el valor del peso del cuerpo.

Como consecuencia de lo expuesto, se puede afirmar que una fuerza es una magnitud vectorial, lo que supone que toda fuerza se puede representar mediante un vector. Asi la fuerza ejercida por la cuerda sobre el cuerpo, se puede representar esquematicamente por un vector (figura 2).

Unidades de fuerza

Cuando una fuerza -F- actúa sobre un cuerpo que puede moverse libremente, éste adquiere una aceleración -a- que depende de su masa. Si modificamos la fuerza, la aceleración también varía, pero de manera que, en cualquier caso, ambas magnitudes permanecen directamente proporcionales, esto es, el cociente -F/a- se mantiene constante:

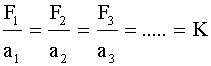
El valor de la constante de proporcionalidad -K- es la masa -m- del cuerpo, por lo que podemos expresar:

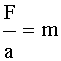
Esta igualdad, que constituye la segunda ley de Newton -tambien denominada Principio de acción de las fuerzas-, la podemos enunciar del siguiente modo:

Cuando sobre un cuerpo que puede moverse libremente actúa una fuerza, el cuerpo adquiere una aceleración (a) de la misma dirección e igual sentido que ella, cuyo valor es directamente proporcional al de la fuerza.

Despejando F de la formula anterior, obtenemos:

F = m · a

Espresión que se conoce como -Principio fundamental de la Dinámica-.

Sistema giorgi.- La unidad de fuerza en el sistema giorgi se denomina Newton (N).

Newton es al fuerza que aplicada a una masa de un kilogramo, le comunica una aceleración de un metro por segundo al cuadrado.

N = Kg · m / s²

Si se sustituye la aceleración general - a - por la aceleración de la gravedad
-g (g = 9,8 m / s²) se obtiene -Fuerza por peso = masa · aceleración gravedad-

Para una masa de 1Kg se obtiene una fuerza por peso de
F = 1 Kg · 9,81 m / s² = 9,81 Kg m / s²

Una masa de 1Kg produce sobre la tierra una fuerza de 9,81 N.

Sistema cegesimal.- La unidad de fuerza en el sistema cegesimal se denomina -dina- (dyn).

Dina es la fuerza que aplicada a una masa de un gramo, le comunica una aceleración de un centrimetro por segundo al cuadrado.

dyn = g · cm / s²

Sistema técnico.- La fuerza es una de las unidades fundamentales del sistema técnico por lo que no se obtiene a partir de otras, si no que se establece como unidad patrón.

El kilogramo fuerza, es la fuerza con la que la Tierra atrae en Paris al kilogramo-masa.

1 Kg = 1 Kgf

Equivalencia entre las unidades

1. Equivalencia entre newton y dina.

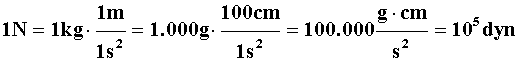
2. Equivalencia entre kilogramo-fuerza y newton.

La tierra ejerce sobre el kilogramo-masa una fuerza de atracción de 1kgf y le imprime una
aceleración de 9,8 m / s².

Cuando una fuerza de 1 N actúa sobre un kilogramo-masa, le imprime una aceleración de 1 m / s².

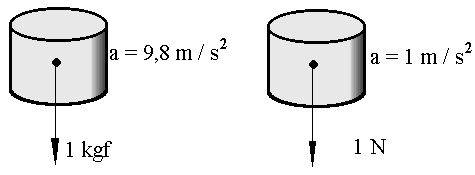
Teniendo en cuenta la proporcionalidad existente entre fuerza y aceleración, podemos expresar:

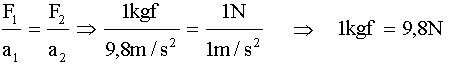
3. Equivalencia entre kilogramo-fuerza y dina.

Considerando las dos relaciones anteriores, resulta:

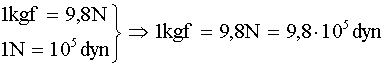
Cuadro resumen de unidades de fuerza

Sistema	Unidades	Equivalencias
Giorgi	newton (N) = kg · m /s²	1 N = 10⁵ dyn 1 kgf = 9,8 N 1 kgf = 9,8 · 10⁵ dyn
Cegesimal	dina (dyn) = g · cm / s²
Tecnico	kgf

Ejercicios

1.	Un coche de 1.200 kg. acelera a razón de 0,8 m / s² . Calcular la fuerza ejercida por el motor.	960 N
2.	Los motores de un avión ejercen sobre este una fuerza de 50.000 kgf. Calcular la aceleración que adquiere si su masa es de 80.000 kg.	6,13 m / s²
3.	Calcular la masa de un cuerpo sabiendo que una fuerza de 8 kgf. le imprime una aceleración de 3 m / s².	26,1 kg

Sistema de fuerzas

Es un conjunto formado por varias fuerzas que actuan simultaneamente sobre un cuerpo.

Composición de fuerzas

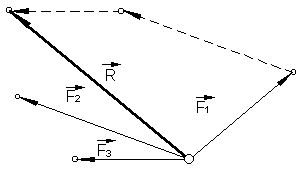
Componer un sistema de fuerzas consiste en hallar una fuerza única que produzca el mismo efecto que todas ellas. A esta fuerza unica se la denomina resultante del sistema.

Para componer un sistema de fuerzas concurrentes, se suman todas ellas como si de vectores de tratara, y la fuerza resultante se aplica en en punto de concurrencia.

En la figura la fuerza R es la resultante de componer F₁, F₂, F₃.

Descomposición de fuerzas

Si deseamos descomponer una fuerza dada, en una suma de otras dos concurrentes, se han de considerar dos casos:

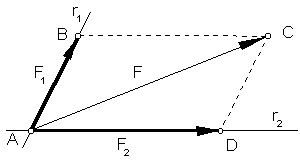
Descomponer la fuerza en dos de direcciones conocidas.

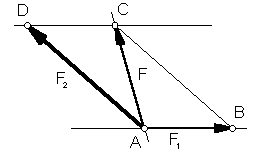
Sea F la fuerza que deseamos descomponer en otras dos de direcciones r₁ y r₂. Para ello trazamos paralelas a ambas direcciones por el extremo de F, con lo que se forma el paralelogramo ABCD, cuyos lados AB y AD son las fuerzas F₁ y F₂ buscadas.

Descomponer la fuerza en suma de otras dos conocida una de ellas.

Sea F la fuerza que deseamos descomponer en otras dos, una de las cuales es F₁ .

Por el extremo de F trazamos una recta paralela a F₁, tomando sobre ella el segmento CD, cuya longitud es igual al módulo de F₁ . El segmento AD asi determinado corresponde a la fuerza F₂, deseada.

Ejercicios

1.	Dos fuerzas de 30 y 40 kgf. tienen sus direcciones perpendiculares. Calcular el módulo de la resultante del sistema constituido por ambas fuerzas.	50 Kgf.
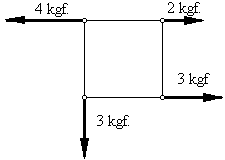
2.	Calcular el módulo de la resultante del sistema de la figura.	3,16 Kgf.
3.	Una fuerza de 100 kgf se desea descomponer en dos que tengan igual módulo y que formen 45 grados con ella. Hallar el módulo de cada una de estas fuerzas.	70,71 kgf.
4.	Hallar el módulo de la resultante del sistema de la figura.	28,3 kgf.
5.	La resultante de dos fuerzas iguales que forman un ángulo de 52º 26' es 84,2 kgf. Calcular el valor de las fuerzas.	46,93 kgf.
6.	Dos fuerzas de 37,4 y 82,6 kgf. tienen una resultante de 116,5 kgf. Calcular el ángulo que forman.	30º