| |
Trabajo, Energía y Potencia |
Trabajo
Si efectuamos una fuerza horizontal sobre una caja apoyada en el suelo, podemos conseguir que ésta se mueva en la dirección y sentido de la fuerza; decimos entonces que hemos realizado un trabajo. Este trabajo es directamente proporcional a la fuerza efectuada y a la distancia recorrida.
El trabajo realizado por una fuerza al desplazarse en su propia dirección es igual al producto que resulta de multiplicar el valor de la fuerza por el espacio recorrido. Se representa por W.
![]()
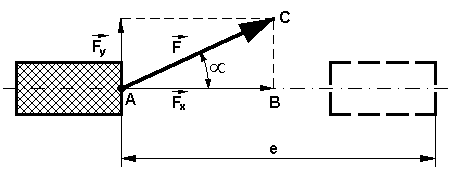
El trabajo realizado por una fuerza, al desplazarse en una dirección cualquiera, es igual al producto que resulta de multiplicar tres factores: el valor de la fuerza, el espacio recorrido y el coseno del ángulo formado por las direcciones de la fuerza y el espacio.
|
|
 |
Unidades de trabajo
Sistema giorgi.- La unidad de trabajo en el sistema giorgi se denomina «julio».
Julio es el trabajo efectuado por una fuerza de un Newton al desplazarse
un metro en su propia dirección.
Se representa por J.
Julio = newton · metro ; J = N · m
Sistema cegesimal.- La unidad de trabajo en el sistema cegesimal se denomina «ergio».
Ergio es el trabajo efectuado por una fuerza de una dina al desplazarse
un centímetro en su propia dirección.
Se representa por erg.
Ergio = dina · centímetro ; erg = dyn · cm
Sistema técnico.- La unidad de trabajo en el sistema técnico se denomina «kilográmetro ».
Kilográmetro es el trabajo efectuado por una fuerza de un
kilogramo-fuerza al desplazarse un metro en su propia dirección.
Se representa por kgm.
Kilogrametro = kilogramo-fuerza · metro ; kgm = kgf · m
Equivalencia entre las unidades.- La equivalencia entre las tres unidades de trabajo se puede obtener fácilmente, sin más que considerar la relación existente entre las correspondientes unidades de fuerza y longitud. Así:
1 J = 1 N · 1 m = 105 dyn · 102 cm = 107 dyn · cm = 107 erg
1 J = 107 erg
1 kgm = 1 kgf · 1 m = 9,8 N · 1 m = 9,8 N · m = 9,8 J
1 kgm = 9,8 J
1 kgm = 9,8 · 107 erg
|
|
Energía
Energía es la capacidad que tienen los cuerpos de producir trabajo.
La energía se manifiesta en muy diversas formas: mecánica, calorífica, eléctrica, luminosa, química... Hasta hace pocos años se pensaba que materia y energía eran dos entes de naturaleza completamente distinta; sin embargo, a principios del presente siglo, el fisicoa mericano Albert Einstein, en su Teoría de la Relatividad, afirmó que la masa se puede trasformar en energía. Esta conclusión, a la que Einstein llegó por procedimientos teóricos, fue confirmada más tarde por la experiencia: la bomba atómica, por ejemplo, no es más que un dispositivo para trasformar en energía una pequeña masa de un material radiactivo. En consecuencia, podemos afirmar: La masa es una forma de manifestación de la energía.
La cantidad total de energía existente en el Universo es siempre la misma, hecho que constituye el «Principio de conservación de la energía»:
La energía no se crea ni se destruye, solamente se trasforma.
Considerando que una energía se mide por la cantidad de trabajo que es capaz de producir, las unidades de energía son idénticas a las unidades de trabajo, anteriormente enunciadas.
Energía mecánica
Es la energía que posee un cuerpo por causas de origen mecánico.Fundamentalmente, se distinguen dos tipos de energía mecánica:
| Energía potencial o de posición. | |
| Energía cinética o de movimiento. |
Energía potencial
Por el simple hecho de ocupar una determinada posición dentro del campo gravitatorio terrestre, un cuerpo posee una energía, ya que si se le permite caer es capaz de efectuar un trabajo. Esta energía se denomina «energía potencial gravitatoria».
Energía potencial es la que posee un cuerpo por el hecho de ocupar una determinada posición dentro de un campo gravitatorio. Se representa por Ep.
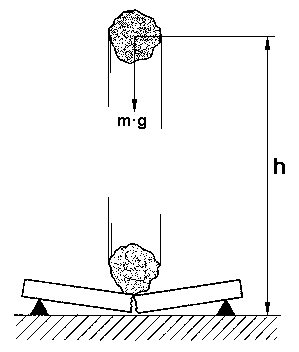 |
Para evaluar la energía potencial que posee un cuerpo de masa m, situado a una altura h en el campo gravitatorio terrestre, nos apoyaremos en el Principio de conservación de la energía. Según él la energía potencial considerada es igual al trabajo que ha sido preciso efectuar para elevar el cuerpo a la expresada altura. Considerando que la fuerza que hay que vencer para elevar el cuerpo es su propio peso: F = P = m · g y que el camino recorrido es la altura h, el trabajo realizado -esto es, la energía potencial del cuerpo- es: Ep = W = F · e = (m · g) h = m · g · h
|
Ejemplo
Calcular la energía potencial que posee un cuerpo de 2 kg de masa, situado a 3 m
de altura.
Sustituyendo en la fórmula anterior, los valores:
m = 2 kg ; g = 9,8 m/s2 ; h = 3 m
todos ellos expresados en unidades del sistema giorgi, resulta:
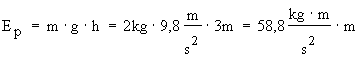
Ep = 58,8 N · m = 58,8 J ; Ep = 58,8 J
Energía cinética
Energía cinética es la que posee un cuerpo por el hecho de
estar en movimiento.
Se representa por Ec.
Considerando que la fuerza necesaria para que, partiendo del reposo, el
cuerpo adquiera una
velocidad v en un tiempo t es:
![]()
y que el espacio recorrido por el cuerpo durante ese tiempo es:
![]()
el trabajo necesario para comunicar al cuerpo la velocidad considerada -esto es, la energía cinética del cuerpo- lo obtendremos multiplicando la fuerza por el espacio:
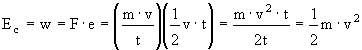
![]()
Ejemplo
Calcular la energía cinética que posee una bala de 4 g de masa, cuando se desplaza con
una velocidad
de 500 m / s.
Sustituyendo en la fórmula los valores:
m = 4 g = 0,004 kg ; v = 500 m/s
expresados en unidades del sistema giorgi, resulta:
Ec= 1/2 m · v2 = 1/2 · 0,004 kg · 250.000 m2 / s2 = 500 J ; Ec = 500 J
|
|
Potencia
Si elevamos una piedra de 20 kgf a 0,8 m de altura, habremos realizado un trabajo:
W = 20 kgf · 0,8m = 16 kgm
Este trabajo es el mismo, independientemente del tiempo que se haya empleado en efectuarlo; sin Embargo, la efectividad de una máquina, o de cualquier otro sistema mecánico, no sólo depende del trabajo que realiza, sino también del tiempo que emplea en llevarlo a cabo. Con objeto de evaluar esta efectividad, definimos una nueva magnitud física denominada «potencia».
Potencia es el cociente entre el trabajo desarrollado por una fuerza y el tiempo empleado en realizarlo. Se representa por P.
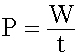
Unidades de potencia
Sistema giorgi.-
La unidad de potencia en el sistema giorgi se denomina «vatio».
Vatio es la potencia desarrollada cuando se realiza un trabajo de
un Julio en un segundo.
Se representa por W.

El vatio posee un múltiplo, denominado kilovatio, que equivale a 1.000 vatios y se representa por kW.
1 kW = 1.000 W
Sistema cegesimal.-
La unidad de potencia en el sistema cegesimal se denomina «ergio
por segundo».
Ergio por segundo es la potencia desarrollada cuando se realiza un trabajo de un
ergio en un segundo.
Sistema técnico.-
La unidad de potencia en el sistema técnico se denomina «kilográmetro por segundo».
Kilográmetro por segundo es la potencia desarrollada cuando se
realiza un trabajo de un
kilográmetro en un segundo. Se representa por kgm / s.
Esta unidad tiene un múltiplo, denominado caballo de vapor,
que equivale a 75 kgm/s
y se representa por CV.
1 CV = 75 kgm / s
Equivalencia entre unidades.-
![]()
![]()
![]()
|
|
Ejercicios
| 1. | Calcular el trabajo necesario para elevar un ascensor de 700 kgf a 20 m de altura. | 14.000 kgm |
| 2. | Expresar en unidades giorgi el resultado del ejercicio anterior. | 137.200 J |
| 3. | Calcular el trabajo que debe realizar una bomba hidráulica para elevar 1 m3 de agua a 12 m de altura. | 12.000 kgm |
| 4. | Calcular la potencia del motor que acciona el ascensor del ejercicio 1, sabiendo que tarda 28 s en efectuar el recorrido. | 500 kgm / s |
| 5. | Calcular la potencia de la bomba del ejercicio 3, sabiendo que eleva 200 litros por minuto. | 40 kgm / s |
| 6. | Un motor de 1 CV se emplea para accionar una grúa que eleva 200 kgf a 15 m de altura. Calcular el tiempo que tardara en efectuar el ascenso. | 40 s |
| 7. | Un tren que pesa 20 000 kgf tarda 45 minutos en subir un puerto de 600 m de desnivel. Calcular la potencia desarrollada por la maquina, en CV. | 59,26 |
| 8. | El cable de un ascensor, cuyo movimiento suponemos uniforme, actúa con una fuerza F cuando asciende con una velocidad v. accionado por un motor cuya potencia es P. Deducir una formula que relacione F, v y P. | P = F · v |
| 9. | Calcular la energía potencial de un cuerpo de 200 g de masa, situado a 50 m de altura. | 98 J |
| 10 | Calcular la energía cinética que posee un cuerpo de 2 kg de masa, cuando se desplaza con una velocidad de 14 m/s. | 196 J |
| 11. | Una bala de 10g, que se desplaza con una velocidad de 500 m/s, atraviesa una plancha metálica de 1 cm de espesor. Calcular la velocidad de la bala después del impacto, sabiendo que la resistencia ofrecida por la plancha es de 800 kgf. | 484 m / s |
| 12. | Calcular la velocidad con que llega al suelo un cuerpo que cae desde una altura h. | |
| 13 | Un barco de vela es empujado por el viento con una fuerza que forma 30º con la dirección del movimiento y cuyo valor es de 600 kgf. Calcular el trabajo realizado cuando el barco haya recorrido 2 km. | 1,4 · 106 kgm |
| 14 | En el ejercicio anterior calcular la potencia desarrollada por el viento cuando el barco avanza con una velocidad de 18 km / h. | 34,6 CV |
| 15. | En electricidad se utiliza el kilovatio-hora como unidad de trabajo, que es el trabajo desarrollado durante una hora por una potencia de un kilovatio. Deducir la equivalencia entre kW-h y kgm. | 1 kW-h = 3,67 · 105 kgm |
| 16. | A cuantos kilovatios equivale 1 CV. | 0,735 kW |
© Roberto de Diego
![]()